This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Rikpratik Sengupta, Department of Physics, Aliah University, Kolkata 700 160, West Bengal, India (E-mail addresses: rikpratik.sengupta@gmail.com(RS))
Table of Links
2. The cosmological model
The Einstein Field Equations (EFE) on the brane have the general form

For the FRW line element describing an isotropic, homogenous universe, the modified EFE on the brane has the form

However, in this letter we shall try to construct a novel non-singular cosmological model of oscillating nature on the spatially flat RS II brane with a spacelike extra dimension (ǫ = 1). For a spacelike extra dimension ǫ being positive, the Hubble parameter does not vanish naturally if the energy density ρ rises upto 2σ. So, RS II cosmology does not contain any inherent feature through which a non-singular bounce can be naturally realized. A Weyl curvature singularity due to infinitely large tidal forces at the wormhole throat can be resolved on the RS II brane with ordinary matter[17]. We shall try to induce the bounce using an ingredient that is quite familiar in early universe cosmology and finds application in achieving the inflationary mechanism- a scalar field. The scalar field is minimally coupled meaning that there is no coupling between the scalar field and gravity. In such a model there may exist an infinite number of cycles containing expansion and contraction phases. However, another additional mechanism is required besides a non-singular bounce to generate such an oscillating universe. The universe must begin to contract at late times following an expanding phase before the next cycle begins. This mechanism is known as the turnaround. We shall use two different mechanisms to generate the bounce and turnaround on the flat RS II brane.

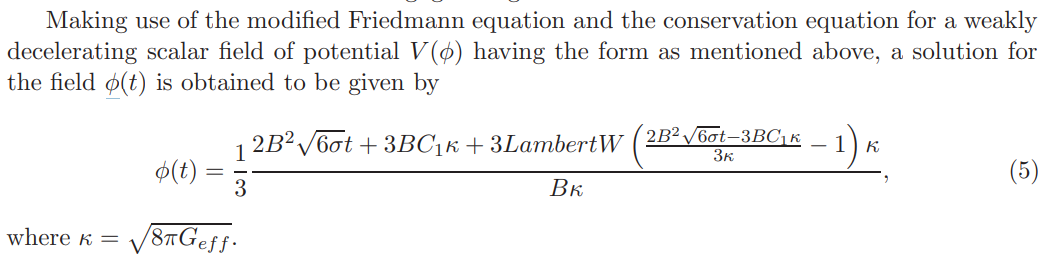
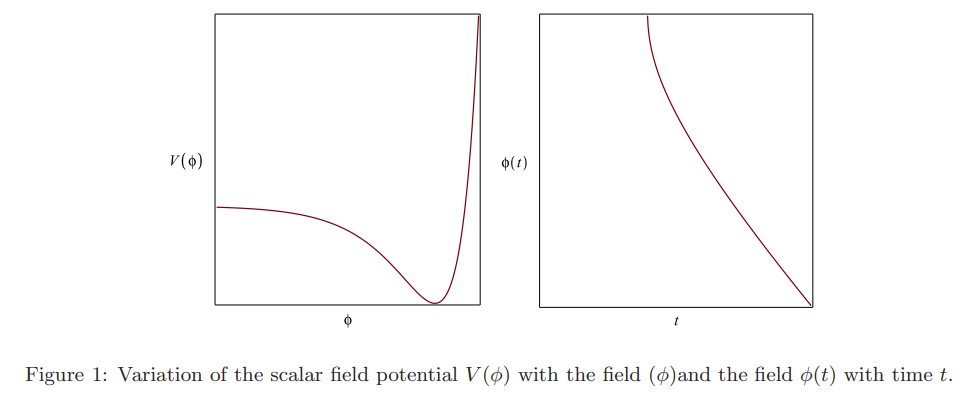
The time evolution of the scalar field has also been plotted in Figure 1. As evident from the figure (estimating the time of the bounce from Figure 2), negative values of the field play an important role in the bounce. So, from the evolution of the potential, it may be said that the bounce happens for the flatter branch of the potential that leads to an emergent cosmology in a closed relativistic Friedmann universe.


We now move on to the late time where the universe is in an accelerating phase. Such a phase has been inferred from astronomical observations[19, 20]. With the discovery of the accelerating universe, there was a resurrection of the Λ-term in cosmology. However, there are certain inconsistencies with the Λ dark energy (DE) that has lead to a wide range of models including quintessence involving scalar fields[21, 22], Chaplygin gas involving fluids with nonlinear equation of states[23, 24] (EoS), the phantom with an exotic EoS[25, 26] and geometrical models which effectively modify the matter sector through geometrical contributions at the infrared (IR) scale[27, 28, 29] but not the real source matter. Here, we have already used a framework in which the geometrical contributions modify the matter sector effectively at the UV scale through the ρ 2 term. If such a term has to be significant in the universe at late times to source a turnaround through its possible non-conventional behaviour (H ∝ ρ), then there has to be a mechanism to make the energy density of the universe grow sufficiently large enough. There is a possibility to achieve this using one of the possible DE candidates that is observationally well favoured-the phantom. The phantom is an exotic fluid with a supernegative EoS (ω < −1) violating the Null Energy condition (NEC), proposed by Caldwell[25] to fit the observational data. The fact tha the phantom fits quite well with the observational data (−1.61 < ω < −0.78) has latter been verified by a number of groups[1, 2, 3].

Again making use of the UV corrected Friedmann equation on the brane, we obtain
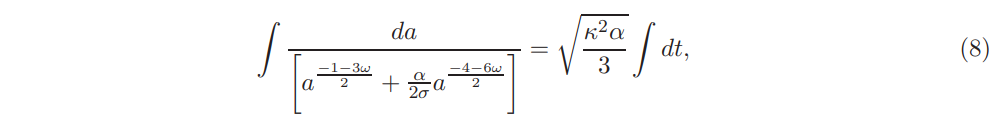
where α is a constant.
We obtain analytical solutions for three different values of the EoS parameter, considering a phantom dominated universe.
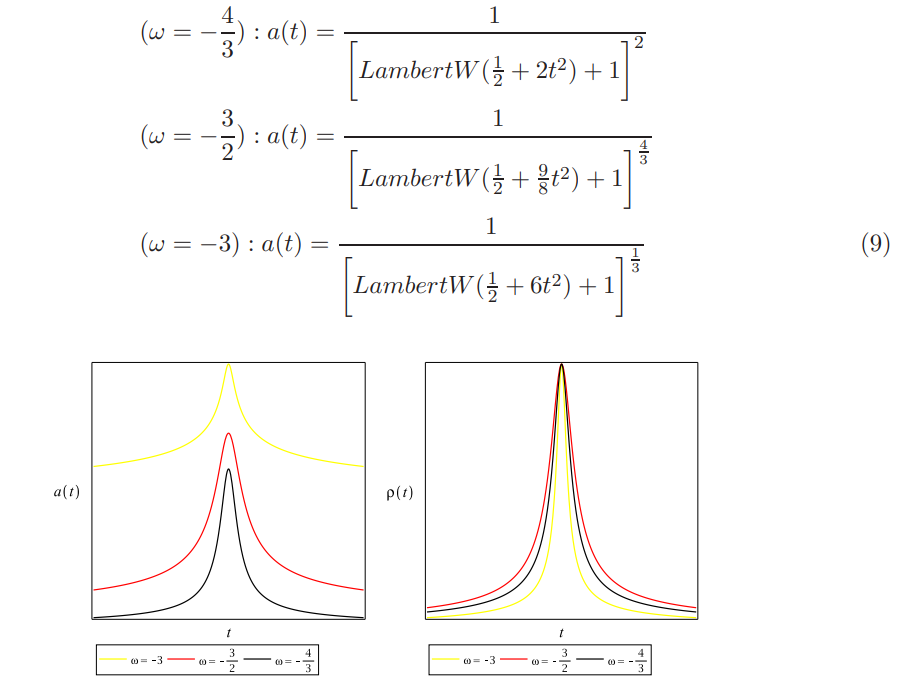
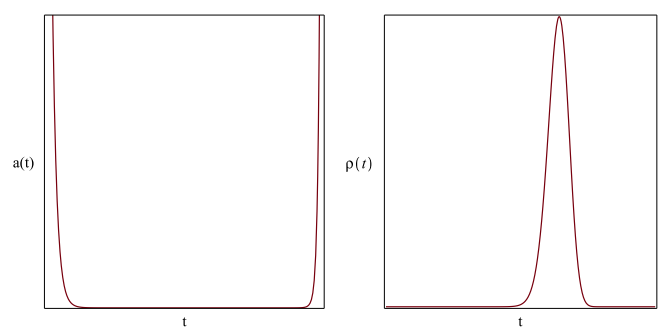
As we find from Figure 3 on plotiing the scale factor with time, the accelerating phantom dominated universe enters into a contracting phase before the scale factor diverges. Once the universe begins to contract, it is dominated by radiation or matter until the scalar field begins to dominate the universe that causes it to bounce before the scale factor reaches a zero value. So, the scale factor maintains a non zero finite value all along the evolution of the universe, never reaching a singular state. The energy density of the universe has also been plotted in Figure 3 as it evolves with time close to the turnaround. It is found to reach a peak just before the turnaround as it keeps on increasing in the phantom dominated eoch, before falling off again. The energy density is large enough at both early and late times to make the quadratic correction term in the modified EFE significant, but never diverges. It starts dropping following both the bounce and turnaround.

